Statistical analysis forms the backbone of modern research, and among the many statistical tools available, the F95 distribution stands out as a crucial concept for researchers, students, and professionals alike. Whether you’re analyzing variance in scientific studies or making critical business decisions, understanding F95 can significantly improve your analytical capabilities.
This comprehensive guide will walk you through everything you need to know about f95, from its basic principles to practical applications. By the end of this article, you’ll have a solid grasp of this important statistical concept and how to apply it in real-world scenarios.
What is F95?
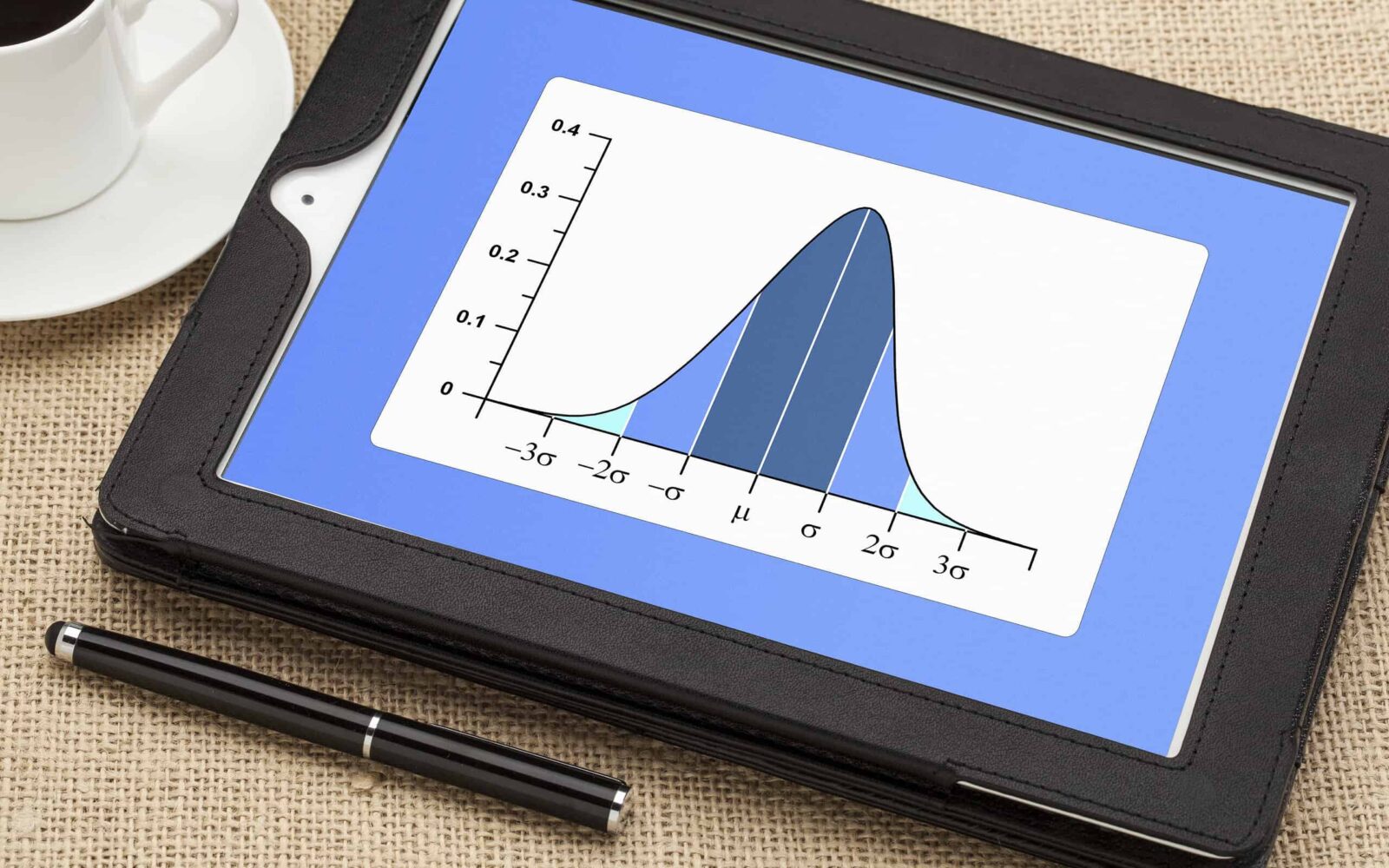
The F95 represents the 95th percentile of the F-distribution, a continuous probability distribution that plays a vital role in hypothesis testing and analysis of variance (ANOVA). Named after Sir Ronald Fisher, the F-distribution helps researchers determine whether the variances between different groups are statistically significant.
When we talk about f95, we’re referring to the critical value that marks the point where 95% of the distribution falls below it. This means that only 5% of values in the distribution exceed this threshold, making it a key benchmark for statistical significance testing.
The F-distribution is characterized by two parameters: degrees of freedom for the numerator (df1) and degrees of freedom for the denominator (df2). These parameters directly influence the shape of the distribution and, consequently, the f95 critical value.
Understanding f95 is essential for anyone working with statistical analysis, as it helps determine whether observed differences in data are due to actual effects or simply random variation. This concept is particularly important in fields like psychology, medicine, engineering, and social sciences.
The Mathematical Foundation of F95
The mathematical basis of f95 stems from the F-distribution’s relationship with chi-square distributions. Specifically, the F-distribution represents the ratio of two independent chi-square random variables, each divided by their respective degrees of freedom.
The probability density function of the F-distribution involves complex mathematical expressions that incorporate gamma functions and the degrees of freedom parameters. However, for practical purposes, most researchers rely on statistical tables or software to determine f95 values rather than calculating them manually.
The critical value f95 varies depending on the degrees of freedom. For instance, with df1=1 and df2=10, the f95 value is approximately 4.96. However, with df1=5 and df2=20, the f95 value drops to about 2.71. This inverse relationship between degrees of freedom and critical values is a fundamental characteristic of the F-distribution.
Modern statistical software automatically calculates f95 values, making it easier for researchers to focus on interpretation rather than computation. Programs like R, SPSS, and Excel all provide built-in functions to determine these critical values accurately.
Applications of F95 in Research
Scientific Research Applications
In scientific research, f95 serves as a cornerstone for hypothesis testing, particularly in experimental design. Researchers use this critical value to determine whether differences between experimental groups are statistically significant or merely due to random chance.
For example, in medical research, scientists might compare the effectiveness of different treatments by analyzing variance between treatment groups. The f95 value helps establish whether observed differences in patient outcomes represent genuine treatment effects or natural variation in the data.
Agricultural scientists frequently employ f95 when testing the effects of different fertilizers, irrigation methods, or crop varieties. By comparing F-statistics to the f95 critical value, they can make informed decisions about which agricultural practices produce significantly better yields.
Environmental researchers also rely on f95 when studying pollution effects, climate variations, or ecosystem changes. This statistical tool helps them distinguish between meaningful environmental impacts and normal fluctuations in natural systems.
Business and Quality Control
In the business world, f95 plays a crucial role in quality control processes. Manufacturing companies use this statistical measure to evaluate whether variations in product quality are within acceptable limits or indicate systematic problems in production.
Service industries apply f95 concepts when analyzing customer satisfaction scores, employee performance metrics, or operational efficiency measures. By comparing variance ratios to f95 critical values, managers can identify areas requiring immediate attention or improvement.
Market research firms utilize f95 when comparing consumer preferences across different demographic groups or geographic regions. This helps businesses make data-driven decisions about product development, marketing strategies, and target audience identification.
How to Calculate and Interpret F95
Step-by-Step Calculation Process
Calculating f95 requires understanding the degrees of freedom for both the numerator and denominator of your F-ratio. The numerator degrees of freedom (df1) typically equal the number of groups minus one, while the denominator degrees of freedom (df2) equal the total sample size minus the number of groups.
Once you’ve determined the degrees of freedom, you can find the f95 critical value using statistical tables, online calculators, or statistical software. Most statistical programs have built-in functions that automatically compute these values when you specify the confidence level and degrees of freedom.
For manual calculation, you would locate the intersection of your df1 (column) and df2 (row) in an F-distribution table at the 0.05 significance level. The value at this intersection represents your f95 critical value.
Interpretation Guidelines
Interpreting f95 results requires comparing your calculated F-statistic to the critical value. If your F-statistic exceeds the f95 critical value, you can reject the null hypothesis and conclude that significant differences exist between groups.
When your F-statistic is less than the f95 critical value, you fail to reject the null hypothesis, suggesting that observed differences might be due to random variation rather than systematic effects.
It’s important to consider the practical significance alongside statistical significance. Even when F-statistics exceed f95, the actual differences between groups might be too small to have meaningful real-world implications.
Common Mistakes When Using F95
Misunderstanding Degrees of Freedom
One of the most frequent errors involves incorrectly calculating degrees of freedom. Many beginners confuse the numerator and denominator degrees of freedom, leading to wrong f95 critical values and invalid conclusions.
Always remember that df1 represents the degrees of freedom for the factor being tested (usually number of groups minus one), while df2 represents the error degrees of freedom (usually total observations minus number of groups).
Double-check your degrees of freedom calculations before looking up f95 values. Incorrect degrees of freedom can completely invalidate your statistical analysis and lead to erroneous conclusions.
Ignoring Assumptions
The F-test and f95 critical values rely on several important assumptions that must be met for valid results. These include normality of data within groups, homogeneity of variance (equal variances across groups), and independence of observations.
Violating these assumptions can make f95 comparisons meaningless and lead to incorrect statistical conclusions. Always test these assumptions before proceeding with F-tests and consider alternative statistical methods if assumptions are violated.
Some researchers overlook the importance of random sampling, which is crucial for the validity of F-test results. Non-random samples can introduce bias that makes f95 comparisons unreliable.
F95 vs Other Statistical Measures
Comparison with t-Distribution
While both the F-distribution and t-distribution are used for hypothesis testing, they serve different purposes. The t-distribution is primarily used for comparing means between two groups, while f95 is used for comparing variances among multiple groups.
The relationship between these distributions is mathematical: the square of a t-statistic with n degrees of freedom equals an F-statistic with 1 and n degrees of freedom. This relationship helps explain why F-tests can be used as alternatives to t-tests in certain situations.
When dealing with only two groups, both t-tests and F-tests will yield equivalent conclusions. However, f95 becomes essential when comparing three or more groups simultaneously, where multiple t-tests would increase the risk of Type I errors.
Z-Score Comparisons
Z-scores and f95 serve different statistical purposes and are not directly comparable. Z-scores standardize individual observations within a distribution, while f95 establishes critical values for comparing group variances.
Understanding when to use each statistical measure is crucial for proper data analysis. Z-scores are appropriate for standardizing data and identifying outliers, while f95 is essential for variance analysis and hypothesis testing.
Both measures assume underlying normal distributions, but they address different research questions and require different interpretation approaches.
Practical Examples of F95 in Action
Educational Research Example
Consider a study comparing the effectiveness of three teaching methods on student performance. Researchers collect test scores from students taught using traditional lectures, interactive workshops, and online modules.
After calculating the F-statistic for the variance between groups, they compare it to the f95 critical value with df1=2 (three groups minus one) and df2=87 (90 total students minus three groups). If the F-statistic exceeds the f95 value of approximately 3.10, they can conclude that teaching methods significantly affect student performance.
This example illustrates how f95 helps educators make evidence-based decisions about instructional strategies and resource allocation.
Medical Research Application
A pharmaceutical company tests four different drug formulations for treating hypertension. They measure blood pressure reductions in patients after treatment and want to determine if any formulation is significantly more effective.
Using ANOVA, they calculate an F-statistic and compare it to the f95 critical value for df1=3 and df2=76. If their F-statistic of 4.85 exceeds the f95 critical value of 2.73, they can conclude that significant differences exist among the drug formulations.
This application demonstrates how f95 supports critical medical decisions that could affect patient outcomes and drug development strategies.
Technology and F95 Calculations
Software Solutions
Modern statistical software has revolutionized how researchers work with f95 calculations. Programs like R, Python (with SciPy), SPSS, and SAS provide built-in functions that automatically calculate F-statistics and compare them to f95 critical values.
These tools eliminate manual calculation errors and allow researchers to focus on data interpretation rather than computational details. Most software packages also provide p-values alongside F-statistics, making it easy to determine statistical significance.
Cloud-based platforms like Google Sheets and online statistical calculators have made f95 calculations accessible to researchers without expensive software licenses. These tools democratize statistical analysis and make advanced techniques available to a broader audience.
Excel and F95
Microsoft Excel offers several functions for working with F-distributions and f95 calculations. The F.INV function calculates critical values, while F.TEST performs two-sample F-tests automatically.
For researchers familiar with Excel, these functions provide a user-friendly way to incorporate f95 analysis into their workflow. Excel’s data analysis toolpak also includes ANOVA functions that automatically compare F-statistics to critical values.
However, Excel has limitations for complex statistical analyses, and researchers working with large datasets or advanced models should consider specialized statistical software for more robust f95 calculations.
Key Takeaways
Understanding f95 is essential for anyone involved in statistical analysis and research. This critical value from the F-distribution serves as a benchmark for determining statistical significance in variance comparisons across multiple groups. Whether you’re a student learning statistics, a researcher analyzing experimental data, or a professional making data-driven decisions, mastering f95 concepts will enhance your analytical capabilities.
The practical applications of f95 span numerous fields, from medical research and quality control to educational studies and business analysis. By properly calculating degrees of freedom, checking statistical assumptions, and interpreting results correctly, you can leverage f95 to make informed decisions based on sound statistical evidence.
Remember that statistical significance doesn’t always equal practical significance, and f95 results should be interpreted within the broader context of your research objectives and real-world implications.
Frequently Asked Questions
What does F95 represent in statistics?
F95 represents the 95th percentile of the F-distribution, serving as a critical value for hypothesis testing. When an F-statistic exceeds the F95 value, it indicates statistical significance at the 0.05 alpha level.
How do I find the F95 critical value for my analysis?
To find F95, you need to know your degrees of freedom for both numerator (df1) and denominator (df2). Use statistical tables, software functions, or online calculators to determine the critical value at the 0.05 significance level.
When should I use F95 instead of other statistical measures?
Use F95 when comparing variances among three or more groups or when conducting ANOVA. For comparing just two groups, t-tests might be more appropriate, though F-tests will yield equivalent results.
What happens if my F-statistic is less than F95?
If your F-statistic is less than F95, you fail to reject the null hypothesis, suggesting that observed differences between groups might be due to random variation rather than systematic effects.
Can I use F95 with non-normal data?
F-tests assume normally distributed data within groups. If your data significantly violates normality assumptions, consider data transformation or alternative non-parametric tests instead of relying on F95 critical values.
For more detailed statistical guidance and research insights, visit World Updates for comprehensive resources on data analysis and research methodologies.
Conclusion
The f95 critical value represents a fundamental concept in statistical analysis that empowers researchers and analysts to make informed decisions about group differences and variance comparisons. Throughout this comprehensive guide, we’ve explored the mathematical foundations, practical applications, and proper interpretation of f95 across various fields and research contexts.
From understanding the basic principles of the F-distribution to recognizing common pitfalls and leveraging modern technology for calculations, mastering f95 concepts provides a solid foundation for rigorous statistical analysis. Whether you’re conducting scientific research, implementing quality control measures, or analyzing business data, the principles outlined in this article will help you apply f95 effectively and interpret results with confidence.
As statistical analysis continues to evolve with new technologies and methodologies, the fundamental importance of f95 remains constant. By combining statistical rigor with practical understanding, you can harness the power of this critical value to drive meaningful insights and evidence-based decision-making in your professional and academic endeavors.













Leave a comment